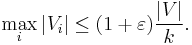Graph partition
In mathematics, the graph partition problem is defined on data represented in the form of a graph G= (V,E), with V vertices and E edges, such that it is possible to partition G into smaller components with specific properties. For instance, a k-way partition divides the vertex set into k smaller components. A good partition is defined such that the number of edges running between separated components is small. Uniform graph partition is a type of graph partitioning problem that consists of dividing a graph into components, such that the components are of about the same size and there are few connections between the components. Important applications of graph partitioning include scientific computing, partitioning various stages of a VLSI design circuit and task scheduling in multi-processor systems.[1] Recently, the uniform graph partition problem has gained importance due to its application for clustering and detection of cliques in social, pathological and biological networks.[2]
Contents |
Problem Complexity
Typically, graph partition problems fall under the category of NP-hard problems. Solutions to these problems are generally derived using heuristics and approximation algorithms.[1][2] However, uniform graph partitioning or a balanced graph partition problem can be shown to be NP-complete.[1]
Problem
Consider a graph G=(V, E), where V denotes the set of n vertices and E the set of edges. For a (k,v) balanced partition problem, the objective is to partition G into k components of at most size v.(n/k), while minimizing the capacity of the edges between separate components.[1] Also, given G and an integer k > 1, partition V into k parts (subsets) V1, V2, ..., Vk such that the parts are disjoint and have equal size, and the number of edges with endpoints in different parts is minimized. Such partition problems have been discussed in literature as bacteria-approximation or resource augmentation approaches. A common extension is to hypergraphs, where an edge can connect more than two vertices. A hyperedge is not cut if all vertices are in one partition, and cut exactly once otherwise, no matter how many vertices are on each side. This usage is common in electronic design automation.
Analysis
For a specific (k,1+ε) balanced partition problem, we seek to find a minimum cost partition of G into k components with each component containing maximum of (1+ε)*(n/k) nodes. We compare the cost of this approximation algorithm to the cost of a (k,1) cut, wherein each of the k components must have exactly the same size of (n/k) nodes each, thus being a more restricted problem. Thus,
We already know that (2,1) cut is the minimum bisection problem and it is NP complete.[3] Next we assess a 3-partition problem wherein n=3k, which is also bounded in polynomial time.[1] Now, if we assume that we have an finite approximation algorithm for (k, 1)-balanced partition, then, either the 3-partition instance can be solved using the balanced (k,1) partition in G or it cannot be solved. If the 3-Partition instance can be solved, then (k, 1)-balanced partitioning problem in G can be solved without cutting any edge. Otherwise if the 3-Partition instance cannot be solved, the optimum (k, 1)-balanced partitioning in G will cut at least one edge. An approximation algorithm with finite approximation factor has to differentiate between these two cases. Hence, it can solve the 3-Partition problem which is a contradiction under the assumption that P=NP. Thus, it is evident that (k,1)-balanced partitioning problem has no polynomial time approximation algorithm with finite approximation factor unless P=NP.[1]
Graph Partition Methods
Since graph partitioning is a hard problem, the solutions are based on heuristics. There are two broad categories of these partitioning approaches. While the first one works locally, the second one considers global connectivity. Well known classical methods for partitioning are the Kernighan–Lin algorithm, and Fiduccia-Mattheyses algorithm which were the first effective 2-way cuts by local search strategies. The major drawback was the arbitrary initial partitioning of the vertex set. The planar separator theorem states that any n-vertex planar graph can be partitioned into roughly equal parts by the removal of O(√n) vertices. This is not a partition in the sense described above, because the partition set consists of vertices rather than edges. However, the same result also implies that every planar graph of bounded degree has a balanced cut with O(√n) edges. Global approaches such as the Spectral partitioning, is based on the spectra of the adjacency matrices.
Multi-level Methods
A multi-level graph partitioning algorithm works by applying one or more stages. Each stage reduces the size of the graph by collapsing vertices and edges, partitions the smaller graph, then maps back and refines this partition of the original graph.[4] A wide variety of partitioning and refinement methods can be applied within the overall multi-level scheme. In many cases, this approach can give both fast execution times and very high quality results. One widely used example of such an approach is METIS,[5] a graph partitioner, and hMETIS, the corresponding partitioner for hypergraphs.[6]
Spectral Partitioning/Spectral Bisection
Given a graph with adjacency matrix A, where an entry Aij implies an edge between node i and j, and degree matrix D, which is a diagonal matrix, where each diagonal entry of a row i, dii, represents the node degree of node i. The Laplacian of the matrix A is defined as L=D-A. Now, a ratio-cut partition for graph G=(V,E) is defined as a partition of V into disjoint U, and W, such that cost of cut(U,W)/(|U|.|W|) is minimized.
In such a scenario, the second smallest eigenvalue (λ) of L, yields a lower bound on the optimal cost (c) of ratio-cut partition with c≥λ/n. The eigenvector (V) corresponding to λ, called the Fiedler vector, bisects the graph into only 2 communities based on the sign of the corresponding vector entry. Division into a larger number of communities is usually achieved by repeated bisection, but this does not always give satisfactory results. The examples in Figures 1,2 illustrate the spectral bisection approach.
Minimum cut partitioning however fails when the number of communities to be partitioned, or the partition sizes are unknown. For instance, optimizing the cut size for free group sizes puts all vertices in the same community. Additionally, cut size may be the wrong thing to minimize since a good division is not just one with small number of edges between communities. This motivated the use of Modularity (networks) (Q) [7] as a metric to optimize a balanced graph partition. The example in Figure 3 illustrates 2 instances of the same graph such that in (a) modularity (Q) is the partitioning metric and in (b), ratio-cut is the partitioning metric.
Other Graph Partition Methods
Spin models have used for clustering of multivariate data wherein similarities are translated into coupling strengths.[8] The properties of ground state spin configuration can be directly interpreted as communities. Thus, a graph is partitioned to minimize the Hamiltonian of the partitioned graph. The Hamiltonian (H) is derived by assigning the following partition rewards and penalties.
- Reward internal edges between nodes of same group (same spin)
- Penalize missing edges in same group
- Penalize existing edges between different groups
- Reward non-links between different groups.
Additionally, Kernel PCA based Spectral clustering takes a form of least squares Support Vector Machine framework, and hence it becomes possible to project the data entries to a kernel induced feature space that has maximal variance, thus implying a high separation between the projected communities [9]
References
- ^ a b c d e f Andreev, Konstantin and R\"{a}cke, Harald, ({2004},). "{Balanced graph partitioning},". {Proceedings of the sixteenth annual ACM symposium on Parallelism in algorithms and architectures}, ({Barcelona, Spain},): {120–124},. doi:{http://doi.acm.org/10.1145/1007912.1007931},.
- ^ a b Sachin B. Patkar and H. Narayanan, (2003,). "An Efficient Practical Heuristic For Good Ratio-Cut Partitioning,". VLSI Design, International Conference on, 0: 64,. doi:{http://doi.ieeecomputersociety.org/10.1109/ICVD.2003.1183116},.
- ^ Garey, Michael R. and Johnson, David S., (1979,). Computers and intractability: A guide to the theory of NP-completeness,. W. H. Freeman & Co.,. ISBN 0716710447,.
- ^ Hendrickson, B. and Leland, R. (1995). "A multilevel algorithm for partitioning graphs". Proceedings of the 1995 ACM/IEEE conference on Supercomputing. ACM. pp. 28.
- ^ Karypis, G. and Kumar, V. (1999). "A fast and high quality multilevel scheme for partitioning irregular graphs". SIAM Journal on Scientific Computing (ACM) 20 (1): 359.
- ^ Karypis, G. and Aggarwal, R. and Kumar, V. and Shekhar, S. (1997). "Multilevel hypergraph partitioning: application in VLSI domain". Proceedings of the 34th annual Design Automation Conference. pp. 526--529.
- ^ Newman, M. E. J. (2006). "Modularity and community structure in networks". PROCEEDINGS- NATIONAL ACADEMY OF SCIENCES USA 103 (23): 8577–8696. doi:10.1073/pnas.0601602103. PMC 1482622. PMID 16723398. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1482622.
- ^ Reichardt, J\"org and Bornholdt, Stefan, (Jul, 2006,). "Statistical mechanics of community detection,". Phys. Rev. E, (American Physical Society,) 74 (1,): 016110,. doi:10.1103/PhysRevE.74.016110,.
- ^ Carlos Alzate and Johan A.K. Suykens, (2010 ,). "Multiway Spectral Clustering with Out-of-Sample Extensions through Weighted Kernel PCA,". IEEE Transactions on Pattern Analysis and Machine Intelligence, (IEEE Computer Society,) 32: 335–347,. doi:http://doi.ieeecomputersociety.org/10.1109/TPAMI.2008.292,. ISSN 0162-8828,.
Bibliography
- BW Kernighan, S Lin (1970). "An efficient heuristic procedure for partitioning graphs". Bell System Technical Journal. http://www.ece.wisc.edu/~adavoodi/teaching/756-old/papers/kl.pdf. One of the early fundamental works in the field. However, performance is O(n2), so it is no longer commonly used.
- CM Fiduccia, RM Mattheyses (1982). "A Linear-Time Heuristic for Improving Network Partitions". Design Automation Conference. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1585498. A later variant that is linear time, very commonly used, both by itself and as part of multilevel partitioning, see below.
- G Karypis, V Kumar (1999). "A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs". Siam Journal on Scientific Computing. http://glaros.dtc.umn.edu/gkhome/node/107. Multi-level partitioning is the current state of the art. This paper also has good explanations of many other methods, and comparisons of the various methods on a wide variety of problems.
- Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999). "Multilevel hypergraph partitioning: applications in VLSI domain". IEEE Transactions on Very Large Scale Integration (VLSI) Systems 7 (1): pp. 69–79. doi:10.1109/92.748202. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=748202. Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design.
- S. Kirkpatrick, C. D. Gelatt Jr., and M. P. Vecchi (13 May 1983). "Optimization by Simulated Annealing". Science 220 (4598): 671–680. doi:10.1126/science.220.4598.671. PMID 17813860. http://www.sciencemag.org/cgi/content/abstract/220/4598/671. Simulated annealing can be used as well.
- Hagen, L. and Kahng, A.B. (September 1992). "New spectral methods for ratio cut partitioning and clustering". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 11, (9): 1074–1085. doi:10.1109/43.159993. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=159993.. There is a whole class of spectral partitioning methods, which use the Eigenvectors of the Laplacian of the connectivity graph. You can see a demo of this, using Matlab.